Dimensionamento de Sistema de Hidrantes: Cálculo Hidráulico Passo a Passo
- rodrigocoimbraproj
- 28 de dez. de 2025
- 24 min de leitura
Atualizado: 29 de dez. de 2025
Introdução – Dimensionamento de Sistema de Hidrantes e Cálculo Hidráulico
O dimensionamento de sistema de hidrantes é uma etapa essencial em projetos de prevenção e combate a incêndio, pois garante que, no pior cenário de operação — normalmente o hidrante mais desfavorável (mais distante e/ou mais elevado) — o sistema forneça vazão e pressão adequadas para o combate manual ao incêndio.
Um projeto de hidrantes bem dimensionado, com cálculo hidráulico correto, reduz significativamente o risco de reprovação junto ao Corpo de Bombeiros, evita retrabalho durante a execução, previne o subdimensionamento de tubulações e também impede o superdimensionamento da bomba de incêndio, que eleva custos e pode comprometer a estabilidade hidráulica do sistema.
Neste artigo, você vai aprender o passo a passo do dimensionamento de hidrantes, com foco exclusivo no cálculo hidráulico do sistema de hidrantes, abordando critérios técnicos como vazão de projeto, perdas de carga, desnível geométrico e pressão residual no esguicho. Na Etapa 2, todos esses conceitos serão aplicados em um exemplo prático completo de dimensionamento de hidrantes, facilitando o entendimento e a replicação do método em outros projetos.
Este conteúdo apresenta um modelo técnico de dimensionamento de sistema de hidrantes com bomba de incêndio de partida elétrica, estruturado de forma que possa ser utilizado como referência padrão em projetos de diferentes tipologias. É importante destacar que, no Brasil, cada estado possui exigências específicas do Corpo de Bombeiros, definidas por Instruções Técnicas, Normas Técnicas ou Normas de Procedimento. Ainda assim, os fundamentos do dimensionamento hidráulico de sistemas de hidrantes — cálculo de vazão, determinação das perdas de carga, análise do hidrante mais desfavorável e definição da altura manométrica total — são universais e podem ser aplicados de forma abrangente, ajustando apenas os parâmetros normativos conforme a legislação local.
Este artigo tem como objetivo apresentar exclusivamente o dimensionamento hidráulico do sistema de hidrantes, não abordando o detalhamento das tubulações, a especificação de componentes, os tipos de equipamentos ou a concepção completa do sistema. O foco está restrito à metodologia de cálculo, servindo como base técnica para engenheiros e profissionais da área.
1) Entenda o Objetivo do Dimensionamento de Sistema de Hidrantes
O dimensionamento de sistema de hidrantes tem como principal objetivo comprovar, por meio de cálculo hidráulico, que o sistema é capaz de atender ao pior cenário de operação, garantindo desempenho adequado durante o combate manual ao incêndio.
Esse pior cenário é representado pelo hidrante mais desfavorável, ou seja, o ponto da rede que apresenta as condições hidráulicas mais críticas. Em geral, trata-se do hidrante mais distante da bomba, mais elevado em relação ao nível de referência ou aquele que concentra maiores perdas de carga ao longo do trajeto hidráulico.
O dimensionamento deve demonstrar que esse hidrante opera corretamente atendendo, simultaneamente, aos seguintes critérios técnicos:
Vazão mínima exigida
A vazão mínima por hidrante é definida pelas normas técnicas e pelas exigências do Corpo de Bombeiros, variando conforme a ocupação da edificação, a carga de incêndio e o tipo de sistema adotado. No cálculo hidráulico, essa vazão representa a condição mínima de operação que deve ser garantida no hidrante mais desfavorável.
Pressão residual mínima no esguicho
Além da vazão, o sistema deve assegurar uma pressão residual mínima no esguicho, suficiente para proporcionar alcance e eficiência do jato de água durante o combate ao incêndio. Essa pressão residual é considerada como uma parcela fixa no cálculo da altura manométrica total e influencia diretamente na seleção da bomba de incêndio.
Funcionamento simultâneo de hidrantes
O dimensionamento hidráulico de hidrantes deve considerar o funcionamento simultâneo de mais de um ponto de consumo. Em grande parte das normas estaduais, adota-se como referência o funcionamento de dois hidrantes simultaneamente. Entretanto, alguns estados exigem a operação simultânea de três ou mais hidrantes, dependendo da área da edificação, do risco da ocupação ou da carga de incêndio.
Esse critério impacta diretamente na vazão total do sistema, sendo um dos fatores mais relevantes no cálculo hidráulico e no dimensionamento da bomba de incêndio.
Reserva de incêndio e bomba compatíveis com o ponto de operação
O dimensionamento também deve garantir que a reserva técnica de incêndio e a bomba de incêndio sejam compatíveis com o ponto de operação do sistema, considerando vazão total e altura manométrica requerida.
Alguns estados apresentam tabelas normativas com volumes mínimos de reservatório pré-definidos, baseados na ocupação e na área de risco da edificação. Ainda assim, do ponto de vista hidráulico, o sistema deve ser capaz de sustentar a vazão exigida durante o tempo mínimo de autonomia, sem queda de desempenho no hidrante mais desfavorável.
Em projetos contra incêndio, o “coração” do dimensionamento é o hidrante mais desfavorável.
Como Identificar o Hidrante Mais Desfavorável
Para o dimensionamento adequado de um sistema de hidrantes, é fundamental identificar corretamente o hidrante mais desfavorável, ou ainda os hidrantes mais desfavoráveis, quando a norma exige o funcionamento simultâneo de mais de um ponto de consumo.
De forma objetiva, o hidrante mais desfavorável é aquele que apresenta as condições hidráulicas mais críticas do sistema, ou seja, o ponto onde ocorrem as maiores perdas de carga totais ao longo do percurso hidráulico. Como consequência direta, é nesse ponto que o sistema tende a apresentar menor pressão disponível e, caso não seja corretamente dimensionado, menor vazão efetiva.
Na prática, o hidrante mais desfavorável geralmente está associado a uma ou mais das seguintes condições:
Maior distância hidráulica em relação à bomba ou à fonte de alimentação, resultando em maiores perdas de carga por atrito na tubulação;
Maior desnível geométrico positivo, ou seja, maior diferença de cota entre o nível de sucção da bomba e a válvula do hidrante;
Maior quantidade de conexões, válvulas ou mudanças de diâmetro ao longo do trajeto, aumentando as perdas localizadas;
Trechos com menores diâmetros, que elevam a velocidade do escoamento e intensificam as perdas de carga.
É importante destacar que o hidrante mais desfavorável nem sempre é apenas o mais distante em planta. Em muitos casos, um hidrante mais próximo, porém localizado em cota superior ou com um trajeto hidráulico mais complexo, pode representar uma condição mais crítica do ponto de vista do cálculo hidráulico de hidrantes.
Quando o dimensionamento exige o funcionamento simultâneo de hidrantes, deve-se identificar a combinação mais desfavorável, ou seja, os pontos que, operando juntos, resultam na maior vazão total demandada e nas maiores perdas de carga no sistema. Essa condição é a que deve ser adotada como base para o cálculo da altura manométrica total e para a seleção da bomba de incêndio.
Identificar corretamente o hidrante mais desfavorável é uma etapa decisiva no dimensionamento de sistema de hidrantes, pois é a partir desse ponto que se valida a capacidade hidráulica do sistema como um todo.
2) Defina o cenário normativo e os critérios do Corpo de Bombeiros
Antes de calcular qualquer coisa, você precisa fixar os parâmetros mínimos exigidos, que mudam conforme:
Estado (IT / NPT / NT)
Tipo de ocupação e risco
Altura e área da edificação
Se há hidrantes internos, externos ou ambos
Nesta etapa você define, pelo menos:
Vazão por hidrante (Q)
Quantidade de hidrantes simultâneos (n)
Pressão residual mínima no esguicho (Pmin)
Diâmetros mínimos permitidos
3) Determine a vazão total do sistema
Depois de obter a vazão por hidrante (Q) e a simultaneidade (n):
Vazão total do sistema:

Exemplo genérico:
Q = 250 L/min por hidrante
n = 2 hidrantes simultâneos→ Qt = 500 L/min
Essa vazão total é a base para:
dimensionar tubulações principais,
escolher bomba,
calcular reserva de incêndio.
4) Escolha o hidrante mais desfavorável
O hidrante mais desfavorável não é “o mais longe” apenas. Geralmente é o ponto que combina:
maior distância hidráulica (maior comprimento equivalente),
maior desnível geométrico (hidrante mais alto),
mais conexões e válvulas no caminho,
e/ou menor diâmetro no trecho final.
Você deve montar o “caminho hidráulico” desde a bomba/reservatório até esse hidrante e calcular as perdas ao longo dele.
5) Faça o traçado hidráulico e levante os comprimentos equivalentes
Monte o trajeto real do escoamento:
tubulação de sucção e recalque
conexões (joelhos, tês, válvulas, reduções).
Aqui, duas coisas são fundamentais:
Comprimento real (L) de cada trecho (em metros)
Comprimento equivalente (Leq) das conexões (ou perda localizada por K, dependendo do método)
No fim, você terá o comprimento total equivalente por trecho/diâmetro:

Comprimentos Equivalentes no Cálculo Hidráulico de Hidrantes
No dimensionamento de sistema de hidrantes, os comprimentos equivalentes são utilizados para representar, de forma simplificada, as perdas de carga hidráulicas geradas por conexões e acessórios da tubulação, como cotovelos, tês, válvulas e reduções.
O conceito de comprimento equivalente consiste em converter a perda de carga localizada de uma conexão em um comprimento fictício de tubulação linear, de mesmo diâmetro, que produza a mesma perda de carga por atrito. Dessa forma, cada conexão é tratada como se fosse um trecho adicional de tubo reto.
Por exemplo, um cotovelo de 4” pode ser considerado hidraulicamente equivalente a aproximadamente 3,76 metros de tubulação linear de mesmo diâmetro. Ao substituir a conexão por esse comprimento adicional, a perda de carga associada ao acessório passa a ser contabilizada juntamente com a perda de carga da tubulação.
Essa abordagem permite simplificar significativamente o cálculo hidráulico de hidrantes, pois evita a necessidade de aplicar fórmulas específicas de perda de carga para cada peça individualmente. Assim, todas as perdas do sistema podem ser avaliadas de forma unificada, utilizando um único método de cálculo por atrito ao longo do comprimento total equivalente da tubulação.



6) Cálculo das Perdas de Carga na Tubulação (Hc)
No dimensionamento de sistema de hidrantes, o cálculo das perdas de carga na tubulação é uma das etapas mais importantes do cálculo hidráulico, pois influencia diretamente a altura manométrica total e a seleção da bomba de incêndio.
O método mais utilizado em redes de hidrantes é a fórmula de Hazen-Williams, por ser adequada ao escoamento de água em regime turbulento e amplamente aceita para tubulações usuais empregadas em sistemas de combate a incêndio.
O cálculo é realizado trecho a trecho, considerando os diâmetros, vazões e comprimentos equivalentes de cada segmento da rede hidráulica. Ao final, todas as perdas são somadas para se obter a perda de carga total na tubulação (Hc).
Fórmula de Hazen-Williams
A perda de carga unitária é obtida pela equação:

Onde:
J = perda de carga unitária (mca/m)
Q = vazão no trecho (m³/s)
C = coeficiente de rugosidade do material da tubulação
D = diâmetro interno da tubulação (m)
Perda de carga em cada trecho
Após determinar a perda unitária, calcula-se a perda de carga do trecho:

Onde:
H(trecho) = perda de carga do trecho (mca)
L = comprimento total equivalente do trecho (m), incluindo tubulação linear e conexões
J = perda de carga unitária (mca/m)
Perda de carga total na tubulação
A perda de carga total na tubulação é obtida pela soma das perdas de todos os trechos analisados:

Esse valor representa a parcela da altura manométrica total associada exclusivamente ao atrito da água com as paredes da tubulação e acessórios, sendo um dos componentes principais do dimensionamento hidráulico de hidrantes.
Critérios de engenharia adotados nesta etapa
Durante o cálculo das perdas de carga, normalmente são definidos critérios de engenharia para garantir eficiência hidráulica e viabilidade econômica do sistema, tais como:
Limitar a velocidade do escoamento, evitando valores excessivos que aumentem as perdas de carga;
Evitar perdas excessivas, que possam resultar em necessidade de bombas maiores e mais onerosas;
Equilibrar o custo da tubulação com o custo da bomba, buscando um ponto de otimização entre diâmetros maiores (menores perdas) e equipamentos de bombeamento.
Esses critérios permitem um dimensionamento de sistema de hidrantes mais eficiente, seguro e economicamente equilibrado, sem comprometer o desempenho hidráulico exigido pelas normas.
7) Cálculo da Perda de Carga na Mangueira (Hm)
No dimensionamento de sistema de hidrantes, a perda de carga na mangueira pode representar uma parcela significativa da altura manométrica total, especialmente em sistemas com mangueiras de maior comprimento ou em vazões elevadas. Em alguns casos, o conjunto mangueira + esguicho pode ser responsável por uma parte relevante da perda total do sistema.
O cálculo da perda de carga na mangueira pode ser realizado por meio da fórmula de Darcy–Weisbach, amplamente aplicada em escoamentos sob pressão. Alternativamente, podem ser utilizadas tabelas fornecidas por fabricantes ou por normas técnicas, desde que compatíveis com a vazão e o diâmetro adotados. Neste artigo, o enfoque permanece no método analítico, por meio da equação completa.
Fórmula de Darcy–Weisbach para a mangueira
A perda de carga na mangueira é dada por:

Onde:
Hₘ = perda de carga na mangueira (mca)
f = fator de atrito da mangueira (adimensional)
Lₘ = comprimento da mangueira (m)
Dₘ = diâmetro interno da mangueira (m)
Vₘ = velocidade da água na mangueira (m/s)
g = aceleração da gravidade (9,81 m/s²)
Para mangueiras de hidrantes, o fator de atrito f é geralmente adotado conforme recomendações normativas ou bibliográficas, sendo comum a utilização de valores típicos para mangueiras flexíveis.
Determinação da velocidade na mangueira
A velocidade do escoamento na mangueira é obtida por:

Onde:
Q = vazão no hidrante (m³/s)
A = área da seção transversal da mangueira (m²)
Dₘ = diâmetro interno da mangueira (m)
Critérios importantes para o dimensionamento
Para que o cálculo da perda de carga na mangueira represente adequadamente a realidade do sistema, é fundamental:
Utilizar o comprimento real da mangueira, conforme previsto no projeto e exigido pela norma;
Adotar corretamente o diâmetro nominal e interno da mangueira, compatível com a vazão de projeto;
Considerar a vazão de operação do hidrante, que corresponde à condição mínima exigida no ponto de consumo;
8) Defina a pressão residual mínima no esguicho (Pmin)
A pressão residual mínima depende do critério normativo e/ou do tipo de esguicho (jato sólido, regulável, neblina, etc.).
No dimensionamento, isso pode entrar como uma parcela fixa necessária no hidrante mais desfavorável:

Normalmente, em esguichos reguláveis, devido às diferenças construtivas e hidráulicas entre fabricantes, a pressão necessária para operação pode variar significativamente de um modelo para outro. A diferença de pressão exigida entre um fabricante “X” e um fabricante “Y” pode ser considerável, mesmo para esguichos de mesmo diâmetro nominal.
Por esse motivo, é essencial que a pressão mínima no esguicho seja determinada com base nos dados técnicos fornecidos pelo fabricante do modelo especificado. Essa pressão deve ser obtida em função da vazão mínima de projeto do hidrante e do alcance mínimo do jato, conforme estabelecido pelas normas e exigências locais do Corpo de Bombeiros.
9) Considere o desnível geométrico (H)
O desnível geométrico é a diferença de cota entre:
nível de sucção
e o ponto de referência do hidrante (ou ponto de consumo)
Conceito:
se o hidrante está acima da bomba → soma (aumenta a altura manométrica)
se está abaixo → reduz

10) Calcule a altura manométrica total requerida (AMT)
Agora você soma tudo para o hidrante mais desfavorável:

Esse valor é a “pressão que a bomba precisa garantir” no ponto de operação.
11) Dimensione a bomba (vazão x altura) e valide o ponto de operação
Com:
Qt (vazão total do sistema)
AMT (altura manométrica total)
Você escolhe uma bomba cuja curva atenda o ponto (Qt, AMT) com margem técnica adequada, sem exageros.
Boa prática:
checar se o ponto fica dentro da faixa eficiente,
avaliar NPSH (quando aplicável),
prever jockey para manutenção de pressão (quando requerido),
e redundância/backup conforme regra local.
12) Checklist final antes de fechar o dimensionamento
Antes de concluir:
o hidrante mais desfavorável atende Q e P?
a rede atende simultaneidade?
perdas localizadas foram consideradas?
diâmetros mínimos e velocidades aceitáveis?
bomba atende (Qt, AMT) no ponto correto?
reserva atende volume e autonomia?
critérios do Corpo de Bombeiros do estado foram cumpridos?
Exemplo de dimensionamento de sistema de hidrantes
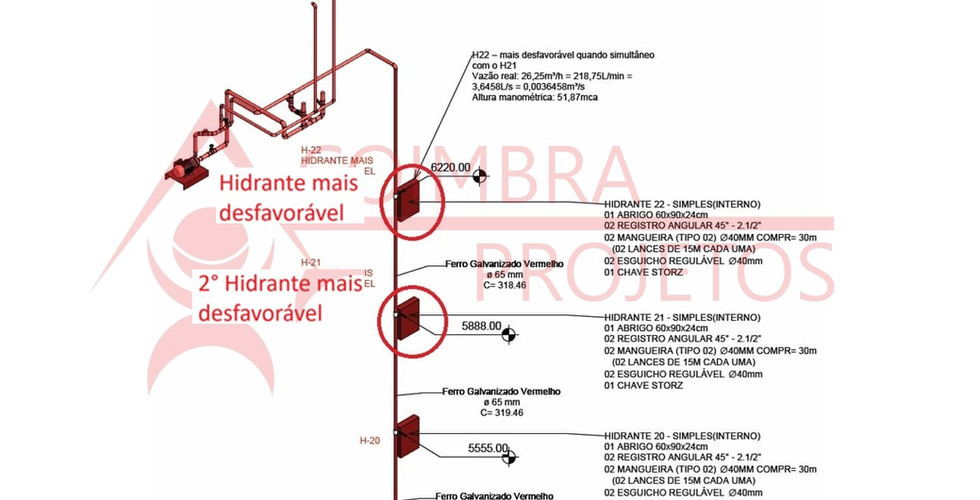
O esquema a seguir será utilizado como base para o exemplo de dimensionamento de um sistema de hidrantes. O foco deste exemplo é exclusivamente o dimensionamento hidráulico do sistema, não abrangendo a especificação de componentes ou a concepção do projeto, partindo-se do pressuposto de que o leitor já possui conhecimento básico sobre o funcionamento de redes de hidrantes.

Definição da Vazão e da Pressão de Projeto
A definição da vazão de projeto e da pressão mínima requerida é a etapa inicial do dimensionamento hidráulico de um sistema de hidrantes. Para isso, é indispensável a análise das normas e instruções técnicas do Corpo de Bombeiros aplicáveis ao local da edificação, uma vez que cada estado estabelece exigências mínimas específicas de vazão, pressão e simultaneidade, de acordo com o tipo de ocupação e o risco envolvido.
Embora os valores normativos possam variar, o método de cálculo hidráulico permanece universal e pode ser aplicado a qualquer situação, bastando adequar os parâmetros de entrada às exigências locais.
Para o exemplo de dimensionamento apresentado neste artigo, serão adotados os seguintes dados mínimos de projeto:
Vazão mínima no hidrante mais desfavorável: 300 L/min
Funcionamento simultâneo: 2 hidrantes
Pressão mínima no esguicho: 20 m.c.a.
A pressão mínima no esguicho deve ser suficiente para garantir o alcance mínimo do jato sólido, conforme exigido pelas normas locais. Em alguns estados do Brasil, essa pressão mínima é exigida diretamente na saída da válvula angular do hidrante, enquanto em outros a exigência é aplicada na ponta do esguicho. Por esse motivo, é fundamental verificar o critério normativo adotado antes de iniciar o cálculo hidráulico.
Identificação do Hidrante Mais Desfavorável em Funcionamento Simultâneo
Com base no esquema hidráulico apresentado anteriormente, o próximo passo do dimensionamento consiste em identificar o hidrante mais desfavorável, bem como o segundo hidrante mais desfavorável, quando a norma exige o funcionamento simultâneo de dois hidrantes.
No dimensionamento hidráulico, o cenário de cálculo deve sempre representar a condição mais crítica de operação do sistema, ou seja, aquela que resulta na maior demanda de vazão total associada às maiores perdas de carga e ao maior desnível geométrico.
No caso deste exemplo, foram identificados os seguintes pontos críticos:
Hidrante H-3: localizado no nível +25 m em relação ao nível de sucção da bomba, caracterizando o hidrante mais desfavorável do sistema;
Hidrante H-2: localizado no nível +20 m em relação ao nível de sucção, representando o segundo hidrante mais desfavorável quando considerado o funcionamento simultâneo.
Assim, o dimensionamento hidráulico será realizado considerando a operação simultânea dos hidrantes H-3 e H-2, uma vez que essa combinação resulta no pior cenário hidráulico para o sistema, sendo determinante para o cálculo das perdas de carga totais, da altura manométrica requerida e da seleção da bomba de incêndio.
Verificação da Velocidade de Escoamento na Sucção e no Recalque
Antes de dar continuidade ao dimensionamento hidráulico do sistema de hidrantes, é indispensável realizar a verificação da velocidade de escoamento nas tubulações de sucção e recalque. Essa verificação tem como objetivo assegurar que o escoamento ocorra dentro de limites aceitáveis, evitando turbulências excessivas, perdas de carga elevadas, risco de cavitação na bomba e instabilidades no funcionamento do sistema.
De acordo com boas práticas de engenharia amplamente adotadas em sistemas de combate a incêndio e em consonância com referências como a NFPA 20, adotam-se os seguintes limites máximos recomendados de velocidade:
Tubulação de sucção: velocidade máxima de 3,0 m/s
Tubulação de recalque: velocidade máxima de 5,0 m/s
Dessa forma, antes de prosseguir com o cálculo das perdas de carga, deve-se verificar se os diâmetros adotados atendem a esses critérios ou se será necessário o redimensionamento das tubulações.
Para este exemplo, foram adotados os seguintes diâmetros:
Sucção: DN 75 mm
Recalque: DN 65 mm
A verificação será realizada considerando a vazão total do sistema, correspondente ao funcionamento simultâneo de dois hidrantes:

Convertendo para o Sistema Internacional:

1) Verificação da Velocidade na Tubulação de Sucção

✅ Condição atendida para a tubulação de sucção.
2) Verificação da Velocidade na Tubulação de Recalque

✅ Condição atendida para a tubulação de recalque.
Caso os limites máximos de velocidade não fossem atendidos, seria necessário aumentar o diâmetro da tubulação e refazer a verificação da velocidade de escoamento, repetindo o procedimento até que os valores obtidos estivessem dentro dos critérios recomendados.
Identificação de trechos, conexões e comprimentos (base do cálculo)
Para facilitar o dimensionamento hidráulico do sistema de hidrantes, a rede é dividida em trechos. Essa divisão permite aplicar o cálculo de perdas de carga de forma organizada, considerando que a vazão muda conforme a simultaneidade:
Trecho de sucção (Qt): do reservatório até a bomba.
Trecho de recalque 1 (Qt): da bomba até o ponto onde ocorre a divisão de vazão para os hidrantes simultâneos (trecho comum, com Qt).
Trecho de recalque 2 (Q): trecho exclusivo até o hidrante mais desfavorável (após a divisão), com Q.
No exemplo, consideramos simultaneidade de 2 hidrantes, então os trechos comuns operam com Qt e os trechos individuais com Q.
Levantamento dos comprimentos totais (Ltotal)
Trecho de sucção — DN 75 mm (0,075 m) — Qt
Comprimentos equivalentes (em metros):
1× entrada de canalização: 1,10 m
1× registro de gaveta: 0,50 m
Comprimento real: 4,00 m

Trecho de recalque 1 — DN 65 mm (0,065 m) — Qt
Comprimentos equivalentes (em metros):
1× válvula de retenção vertical: 8,10 m
1× registro de gaveta: 0,40 m
2× tê passagem direta: 2×1,30=2,60 m
4× cotovelo 90°: 4×2,00=8,00 m
Comprimento real: 38,00 m

Trecho de recalque 2 — DN 65 mm (0,065 m) — Q
Comprimentos equivalentes (em metros):
1× válvula angular: 8,10 m
1× tê passagem direta: 1,30 m
1× cotovelo 90°: 2,00 m
Comprimento real: 5,50 m

Desnível geométrico até o H-3

Perda de carga na tubulação (Hc) com Hazen-Williams
A perda de carga total na tubulação será:

Para cada trecho, usando Hazen-Williams na forma de perda total:

Onde:
H em mca
L em m
Q em m³/s
C=120 (adotado)
D em m
Atenção: nos trechos com simultaneidade, a vazão é 2Q (Qt). No trecho individual, a vazão é Q.
Expressão geral de Hazen–Williams aplicada aos trechos
Nota: neste artigo, as perdas de carga distribuídas na tubulação são calculadas pelo método de Hazen-Williams, que resulta em uma perda proporcional à vazão elevada à potência 1,85. Por isso, em trechos com simultaneidade (trecho comum), a vazão considerada é a vazão total do sistema (Qt), enquanto no trecho exclusivo do hidrante mais desfavorável a vazão é apenas a vazão por hidrante (Q). Ao final, as perdas de todos os trechos são somadas para compor Hc.
A perda de carga em um trecho qualquer é dada por:

Aplicando essa equação a cada trecho, obtêm-se as seguintes expressões:
Perda de carga no trecho de sucção

Perda de carga no trecho de recalque comum

Perda de carga no trecho de recalque individual
Neste trecho, a vazão é metade da vazão total do sistema:

Substituindo na equação de Hazen–Williams:

Aplicando a propriedade de potências:

Logo:

Soma das perdas de carga na tubulação
Somando os três termos:

Observa-se que o termo Qt^1,85 é comum a todas as parcelas e pode ser colocado em evidência.
Substituição dos valores geométricos e normativos
Para o exemplo em estudo, foram adotados:


Resultado do coeficiente global da tubulação
Efetuando os cálculos numéricos de cada parcela e somando os resultados, obtém-se:

Equação parcial final da perda de carga na tubulação
Assim, a perda de carga total na tubulação, expressa corretamente em função da vazão total do sistema, é:

Cálculo da Perda de Carga na Mangueira (Hm)
Para a determinação da perda de carga na mangueira, utiliza-se a equação de Darcy–Weisbach, conforme já discutido anteriormente. Esse método é particularmente adequado para mangueiras de hidrantes, uma vez que considera explicitamente a velocidade do escoamento e o fator de atrito.
No exemplo em análise, adotam-se os seguintes dados de projeto:
Comprimento da mangueira (Lm): 30,00 m
Diâmetro nominal: 1½" (40 mm)
Diâmetro interno adotado para cálculo: 0,040 m
Fator de atrito (f): 0,022
Aceleração da gravidade (g): 9,81 m/s²
Ressalta-se que, para efeitos de cálculo hidráulico rigoroso, devem ser utilizados os diâmetros internos reais fornecidos pelo fabricante da mangueira. Neste exemplo, o valor adotado possui finalidade exclusivamente didática.
Equação de Darcy–Weisbach
Nota: a perda de carga na mangueira é calculada por Darcy–Weisbach, onde a velocidade é obtida pela razão entre vazão e área. Como a mangueira alimenta apenas um hidrante por vez, a vazão na mangueira é sempre Q (vazão por hidrante), mesmo quando o sistema opera com dois hidrantes simultaneamente (Qt). Esse detalhe é essencial para manter a consistência matemática da equação final.
A perda de carga na mangueira é dada por:

A velocidade média na mangueira pode ser expressa em função da vazão:

Mas atenção: a mangueira trabalha com a vazão de um hidrante, e como o sistema tem 2 hidrantes simultâneos:

Logo, a velocidade na mangueira em função de Qt fica:

Substituindo na Darcy–Weisbach


Cálculo numérico do coeficiente Km

Pressão Mínima no Esguicho (Pmin)
Por fim, considera-se a pressão mínima requerida no esguicho, que constitui uma das parcelas fixas da altura manométrica total do sistema. Conforme já discutido anteriormente, no caso de esguichos reguláveis, a pressão mínima de operação deve ser obtida diretamente a partir dos dados técnicos fornecidos pelo fabricante, uma vez que diferenças construtivas podem resultar em variações significativas de desempenho entre modelos distintos.
Para esguichos do tipo tronco cônico — que não são o foco deste exemplo, mas permanecem como alternativa técnica — a pressão mínima pode ser estimada por meio da seguinte relação empírica:

Onde:
hp,esg = pressão mínima no esguicho (mca)
Q = vazão no esguicho (m³/s)
No entanto, reforça-se que, para esguichos reguláveis, essa abordagem não substitui os dados do fabricante, devendo ser utilizada apenas quando aplicável e normativamente aceita.
No presente exemplo de dimensionamento, será adotada uma pressão mínima no esguicho de 20 mca, valor compatível com as exigências normativas e que apresenta margem técnica adequada em relação às pressões mínimas indicadas por fabricantes de esguichos reguláveis disponíveis no mercado brasileiro.
Temos:

Fechamento da Equação da Altura Manométrica Total (AMT)
Após o desenvolvimento individual de cada parcela que compõe o dimensionamento hidráulico do sistema de hidrantes, torna-se possível reunir todos os termos em uma única expressão matemática, denominada Equação da Altura Manométrica Total (AMT). Essa equação representa a carga total que a bomba de incêndio deve vencer para garantir o funcionamento adequado do sistema no pior cenário de operação.
De forma geral, a altura manométrica total é definida por:
Relembrando a expressão geral:

onde:
Hc corresponde à perda de carga total na tubulação;
Hm corresponde à perda de carga na mangueira;
Δz é o desnível geométrico entre a sucção da bomba e o hidrante mais desfavorável;
Pmin é a pressão residual mínima exigida no esguicho.
Onde cada termo já foi definido e expresso em função da vazão.
Parcela das perdas de carga na tubulação (Hc)
Conforme demonstrado detalhadamente anteriormente, a perda de carga na tubulação, expressa corretamente em função da vazão total do sistema (Qt), é dada por:

Esse termo incorpora:
as perdas nos trechos comuns da rede, operando com vazão total Qt;
as perdas no trecho individual do hidrante mais desfavorável, operando com vazão Qt/2;
as características geométricas e hidráulicas da tubulação do sistema.
Parcela da perda de carga na mangueira (Hm)
A perda de carga na mangueira foi obtida a partir da equação de Darcy–Weisbach, considerando que a mangueira opera com a vazão de um único hidrante, ou seja, Qt/2.
Após o desenvolvimento matemático apresentado anteriormente, a expressão da perda de carga na mangueira, reescrita em função da vazão total do sistema, resulta em:

Esse termo representa a parcela concentrada de perda de carga associada ao conjunto mangueira e esguicho, sendo diretamente proporcional ao quadrado da vazão.
Termos independentes da vazão
Os termos que não dependem da vazão do sistema são:
🔹 Desnível geométrico
Considerando que o hidrante mais desfavorável encontra-se a uma cota superior em relação à sucção da bomba, o desnível geométrico é:

🔹 Pressão residual mínima no esguicho
Com base nos dados do fabricante do esguicho regulável adotado e nas exigências normativas, foi considerada uma pressão residual mínima de:

Somando-se ambos:

Equação final da Altura Manométrica Total
Reunindo todas as parcelas desenvolvidas, obtém-se a equação final da altura manométrica total, expressa em função da vazão total do sistema:

Interpretação da equação da AMT
A equação acima representa o comportamento hidráulico completo do sistema de hidrantes no pior cenário de operação, permitindo:
traçar a curva do sistema (altura manométrica × vazão);
comparar diretamente essa curva com a curva característica da bomba de incêndio;
verificar se a bomba selecionada atende simultaneamente à vazão total requerida e à altura manométrica necessária;
avaliar margens de segurança e eventuais ajustes de diâmetro ou equipamentos.
É importante destacar que essa equação já considera o funcionamento simultâneo de dois hidrantes, bem como todas as perdas distribuídas e concentradas relevantes para o dimensionamento hidráulico.
A partir da equação da altura manométrica total, torna-se possível selecionar a bomba de incêndio de forma precisa, garantindo que o sistema de hidrantes atenda integralmente às exigências hidráulicas no pior cenário de operação, sem superdimensionamentos ou incertezas técnicas.
Substituição Numérica da Equação da AMT para a Vazão de Projeto
Definição da vazão mínima de projeto
Para a vazão mínima de projeto, considera-se Q=300 L/min por hidrante e simultaneidade de 2 hidrantes, resultando em Qt=600 L/min. Substituindo Qt na equação final da AMT, obtém-se AMT≈69,5 mca. Esse ponto (600 L/min, ~70 mca) é o ponto mínimo de projeto usado para seleção da bomba.
Conforme definido no exemplo:
Vazão mínima por hidrante:
Q=300 L/min
Funcionamento simultâneo de dois hidrantes:
Qt=2Q=600 L/min
Convertendo para unidades do Sistema Internacional:
Qt=600/1000×60=0,0100 m3/s
Cálculo termo a termo da equação
🔹 Termo das perdas de carga na tubulação

🔹 Termo da perda de carga na mangueira

🔹 Termos independentes da vazão

Altura Manométrica Total requerida
Somando todas as parcelas:

Resultado final do dimensionamento hidráulico
Para a vazão mínima de projeto adotada, o sistema de hidrantes requer:
Vazão total do sistema:

Altura manométrica total requerida:

Seleção da bomba de incêndio
Com a vazão mínima de projeto e a altura manométrica total determinadas, torna-se possível realizar a seleção da bomba de incêndio.
A bomba escolhida deve atender, no mínimo, ao ponto de operação definido por:
Vazão: 600 L/min
Altura manométrica: aproximadamente 70 mca
Esse ponto deve estar dentro da faixa operacional da bomba, preferencialmente próximo à região de maior eficiência hidráulica da curva característica do equipamento, evitando tanto o subdimensionamento quanto o superdimensionamento.
A partir dessa verificação, pode-se validar o conjunto motobomba, bem como analisar requisitos complementares, como potência instalada, regime de funcionamento e critérios normativos aplicáveis.
Assim, com a definição da vazão mínima de projeto e da altura manométrica total, o dimensionamento hidráulico do sistema de hidrantes encontra-se concluído, permitindo a seleção adequada da bomba de incêndio capaz de atender plenamente ao pior cenário de operação do sistema.
Funcionamento real do sistema e determinação da vazão de operação
Até este ponto, o dimensionamento hidráulico do sistema de hidrantes permitiu determinar a altura manométrica total mínima requerida para atender o pior cenário de operação, correspondente ao funcionamento simultâneo de dois hidrantes.
Entretanto, é importante destacar que, na operação real, a bomba de incêndio não trabalha exatamente na vazão mínima de projeto. O ponto de funcionamento efetivo do sistema depende da interação entre:
a curva do sistema, representada pela equação da altura manométrica total (AMT);
a curva característica da bomba, fornecida pelo fabricante, associada a um determinado rotor e rotação.
O ponto de operação real ocorre no cruzamento entre essas duas curvas, e é nesse ponto que se obtém simultaneamente:
a vazão real de funcionamento do sistema;
a altura manométrica efetivamente fornecida pela bomba.
Curva do sistema (AMT)
A curva do sistema é obtida diretamente a partir da equação da altura manométrica total desenvolvida neste artigo:

Essa equação permite calcular a altura manométrica exigida para qualquer valor de vazão total Qt, possibilitando a construção do gráfico Altura Manométrica × Vazão do sistema.

Curva da bomba e ponto de operação
A curva da bomba representa a relação entre vazão e altura manométrica fornecida pelo equipamento, sendo uma característica própria de cada modelo, rotor e rotação. Em geral, trata-se de uma curva decrescente, na qual a altura disponível diminui à medida que a vazão aumenta.
Ao sobrepor a curva do sistema à curva da bomba, obtém-se um ponto de interseção que define o ponto de operação real do conjunto motobomba.
No gráfico apresentado, observa-se:
o ponto mínimo de projeto, correspondente a 600 L/min e aproximadamente 69,5 mca, utilizado como referência para o dimensionamento;
o cruzamento entre a curva do sistema e a curva da bomba, que indica a vazão real de funcionamento, normalmente superior à vazão mínima adotada em projeto.
Esse comportamento é esperado e desejável, desde que a vazão real não ultrapasse limites normativos ou operacionais do sistema.
Interpretação técnica do gráfico
A análise conjunta das curvas permite concluir que:
a bomba selecionada atende ao ponto mínimo de projeto exigido pelo sistema;
a vazão real de operação é determinada automaticamente pela interação hidráulica entre bomba e sistema;
pequenas variações na curva da bomba (troca de rotor, ajuste de rotação) alteram diretamente o ponto de operação, sem comprometer o atendimento ao requisito mínimo de projeto.
Assim, o dimensionamento hidráulico garante que, independentemente da vazão real resultante, o sistema sempre opere acima das condições mínimas exigidas no hidrante mais desfavorável.
Com a determinação da equação da altura manométrica total e a análise gráfica da curva do sistema em conjunto com a curva da bomba, conclui-se o dimensionamento hidráulico do sistema de hidrantes. A seleção adequada da bomba assegura que o sistema atenda às exigências mínimas de vazão e pressão, enquanto o ponto de operação real define a vazão efetiva de funcionamento, garantindo segurança, eficiência hidráulica e confiabilidade operacional.
Por que não foi calculada a potência mínima da bomba neste artigo?
É comum encontrar, em projetos de sistemas de hidrantes, a exigência ou a apresentação da chamada “potência mínima da bomba” como um dado principal do dimensionamento. No entanto, essa prática, embora difundida ao longo do tempo, não representa o critério técnico mais adequado para a seleção da bomba de incêndio.
O fator determinante no dimensionamento hidráulico de um sistema de hidrantes não é a potência do motor, mas sim a capacidade da bomba de fornecer a vazão e a altura manométrica mínimas exigidas no ponto de operação do sistema.
Em outras palavras, o sistema não “enxerga” potência: ele exige vazão (Qt) e pressão (AMT).
“A potência do motor não é critério de desempenho hidráulico; é consequência da eficiência do conjunto bomba + ponto de operação.”
O equívoco do “dimensionamento por potência mínima”
O uso da potência mínima como critério principal de projeto é um equívoco comum entre projetistas e órgãos fiscalizadores, pois:
a potência não define o desempenho hidráulico do sistema;
bombas diferentes podem atender a mesma vazão e pressão, porém com potências distintas;
a potência está diretamente relacionada à eficiência hidráulica da bomba, e não apenas à carga do sistema.
Assim, dois fabricantes distintos podem fornecer bombas que atendem exatamente ao mesmo ponto de projeto (vazão × altura), sendo que:
uma bomba pode exigir, por exemplo, 10 CV;
outra, mais eficiente, pode exigir apenas 7,5 CV.
Ambas estão corretas do ponto de vista hidráulico, desde que atendam ao ponto de operação exigido.
A potência está ligada à eficiência da bomba
A potência absorvida pela bomba depende fundamentalmente de sua eficiência global, que envolve:
eficiência hidráulica;
eficiência volumétrica;
eficiência mecânica.
Por esse motivo, a potência não é um parâmetro absoluto do sistema, mas sim uma consequência da escolha do equipamento.
Exigir uma “potência mínima” fixa, sem analisar a curva real da bomba, pode levar a:
superdimensionamento do motor;
aumento desnecessário de custos;
menor eficiência energética do conjunto.
Fórmula teórica da potência da bomba
Do ponto de vista conceitual, é possível estimar a potência necessária por meio da expressão clássica:
Potência hidráulica (em CV)

Onde:
Pcv = potência da bomba (CV)
ρ = densidade da água (≈ 1000 kg/m³)
g = aceleração da gravidade (9,81 m/s²)
Q = vazão (m³/s)
H = altura manométrica total (m)
η = eficiência global da bomba (adimensional)
75 = fator de conversão para cavalo-vapor (CV)
De forma simplificada, para água:
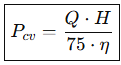
Limitação prática da fórmula
Embora essa fórmula permita uma estimativa teórica, ela apresenta uma limitação importante:
👉 a eficiência η depende da bomba escolhida, e não do sistema.
Ou seja, sem conhecer a curva real do fabricante, qualquer valor de potência obtido por essa equação será apenas uma aproximação, muitas vezes conservadora.
Critério correto adotado na prática profissional
Na prática atual de engenharia contra incêndio, o procedimento tecnicamente correto é:
Determinar a vazão mínima de projeto (Qt)
Determinar a altura manométrica total (AMT)
Selecionar a bomba cuja curva atenda esse ponto
Adotar a potência do motor conforme indicado pelo fabricante, para o ponto de operação obtido
Esse método garante que:
o sistema atenda integralmente às exigências hidráulicas;
a bomba opere dentro da sua faixa de eficiência;
a potência instalada seja adequada e realista.
Portanto, a ausência do cálculo da potência mínima neste artigo não representa uma falha de dimensionamento, mas sim uma escolha técnica consciente. O critério fundamental para a seleção da bomba de incêndio é o atendimento à vazão e à altura manométrica exigidas pelo sistema. A potência do motor deve ser definida a partir da bomba selecionada, conforme dados do fabricante, refletindo a eficiência real do equipamento e garantindo desempenho hidráulico adequado.
Conclusão
O dimensionamento de um sistema de hidrantes vai muito além da simples aplicação de fórmulas ou da repetição de cálculos padronizados. Embora a matemática seja parte essencial do processo, ela é apenas a ferramenta que materializa decisões técnicas tomadas com base no entendimento profundo do funcionamento do sistema, do comportamento hidráulico da rede e das condições reais de operação.
Cada escolha feita ao longo do dimensionamento — definição do hidrante mais desfavorável, consideração da simultaneidade, análise das perdas de carga, interpretação das curvas de bomba e do ponto de operação — exige conhecimento técnico, senso crítico e responsabilidade profissional. O cálculo, por si só, não garante um sistema seguro; é a engenharia por trás dele que assegura desempenho, confiabilidade e conformidade normativa.
A matemática aplicada ao dimensionamento hidráulico é elegante e precisa, mas o processo que conduz aos resultados não é simples nem mecânico. Ele exige experiência, interpretação correta das normas, compreensão do comportamento dos equipamentos e domínio dos princípios hidráulicos envolvidos.
Tratar o dimensionamento de sistemas de hidrantes como um “mero cálculo” é desconhecer a complexidade e a responsabilidade inerentes à engenharia de prevenção e combate a incêndio. O verdadeiro profissional alia cálculo, engenharia e conhecimento técnico com rigor e profissionalismo, pois, em última análise, está projetando sistemas que protegem patrimônios e, principalmente, vidas.










Comentários